Can A Function Cross A Horizontal Asymptote? Exploring Limits In Mathematics
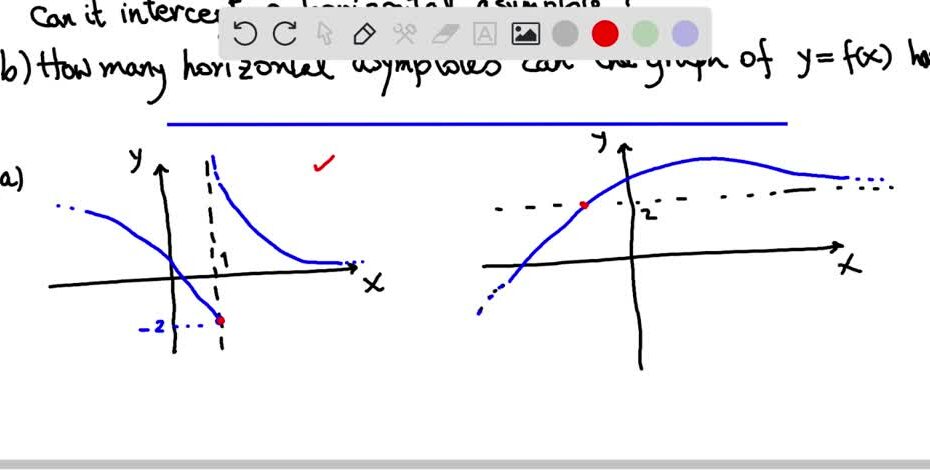
Determine Whether A Graph Intersects The Horizontal Asymptote 143-4.2.4.C
Keywords searched by users: Can a function intersect a horizontal asymptote how many horizontal asymptotes can a function have in maximum?, the graph of a rational function can never cross a horizontal asymptote, can a rational function cross a slant asymptote, why can’t vertical asymptotes be crossed, horizontal asymptote examples, horizontal asymptote on graph, how to draw horizontal asymptote, how to interpret horizontal asymptote
Can Functions Cross Horizontal Asymptotes?
Can functions cross horizontal asymptotes? Horizontal asymptotes represent the behavior of a function as x-values approach positive or negative infinity. It is important to note that a rational function cannot cross a vertical asymptote because doing so would involve dividing by zero, which is mathematically undefined. However, when it comes to horizontal asymptotes, they serve as a guideline for the long-term behavior of the function as x-values become extremely large in either the positive or negative direction. Unlike vertical asymptotes, horizontal asymptotes can indeed be crossed by a function. This means that a function can approach and then cross a horizontal asymptote as it continues to evolve with increasing or decreasing x-values. This phenomenon adds an interesting dimension to understanding how functions behave in the long run.
Can An Asymptote Intersect The Function?
Can a function’s graph intersect a vertical asymptote? To answer this question, we need to consider the concept of continuity. In mathematics, a function is considered continuous at a point ‘a’ in its domain if the limit of the function as ‘x’ approaches ‘a’ is equal to the function’s value at ‘a.’ In other words, lim(x→a) f(x) = f(a).
Now, when it comes to vertical asymptotes, it’s important to understand that these are essentially lines that a function’s graph approaches but never touches or crosses. In order for a function’s graph to intersect a vertical asymptote, it would need to contain a point that lies directly on the asymptote itself. However, due to the definition of continuity mentioned earlier, this is not possible because the limit and the function’s value must match at every point in the domain for the function to be considered continuous. Therefore, a function’s graph cannot intersect a vertical asymptote.
Update 10 Can a function intersect a horizontal asymptote







Categories: Update 30 Can A Function Intersect A Horizontal Asymptote
See more here: maucongbietthu.com

Assuming you mean a horizontal (or oblique) asymptote, absolutely yes. For example, the function is asymptotic to as , but crosses it infinitely many times. No graph crosses a vertical asymptote since the function is not defined at that point. Graphs can cross horizontal and slant asymptotes.A rational function cannot cross a vertical asymptote because it would be dividing by zero. Horizontal asymptotes occur when the x-values get very large in the positive or negative direction. Horizontal asymptotes can be crossed.So, the function’s graph cannot intersect the vertical asymptote because in order for it to do so, the graph should contain a point on the asymptote. Definition: A function f:D→R is continuous at a point a in its domain D if limx→af(x)=f(x).
Learn more about the topic Can a function intersect a horizontal asymptote.
- Is it possible for an asymptote to intersect with its graph? – Quora
- 2-07 Asymptotes of Rational Functions
- Can a graph of a continuous function intersect its vertical …
- Can a horizontal asymptote be intersected more than once? If so …
- Determine Whether a Graph Intersects the Horizontal Asymptote 143-4.2.4.c
- 1.4: Limits at Infinity and Horizontal Asymptotes : End Behavior