Can A Finite Set Defy Countability?

Can finite sets be classified as either countable or uncountable? By definition, a finite set is considered countable. However, if your understanding of countability differs from this definition, please provide specifics so that we can offer a more tailored explanation. If you define countable as encompassing sets that are either finite or enumerable, then, by this very definition, a finite set is indeed countable. This concept holds true based on the standard understanding of countability in set theory. The information provided here is as of May 20, 2019.

An illustrative instance of an uncountable finite set can be found in the set of real numbers ranging from 0 to 1. This set is considered uncountable due to the fundamental fact that, regardless of how hard you try, it will perpetually contain an infinite number of elements, and you can never list them all exhaustively. Consequently, this set lacks a one-to-one correspondence with the set of natural numbers, further emphasizing its uncountable nature. In essence, an uncountable finite set, like the one described here, showcases how certain mathematical sets possess an unbounded, infinite quality despite having a finite interval or boundary.

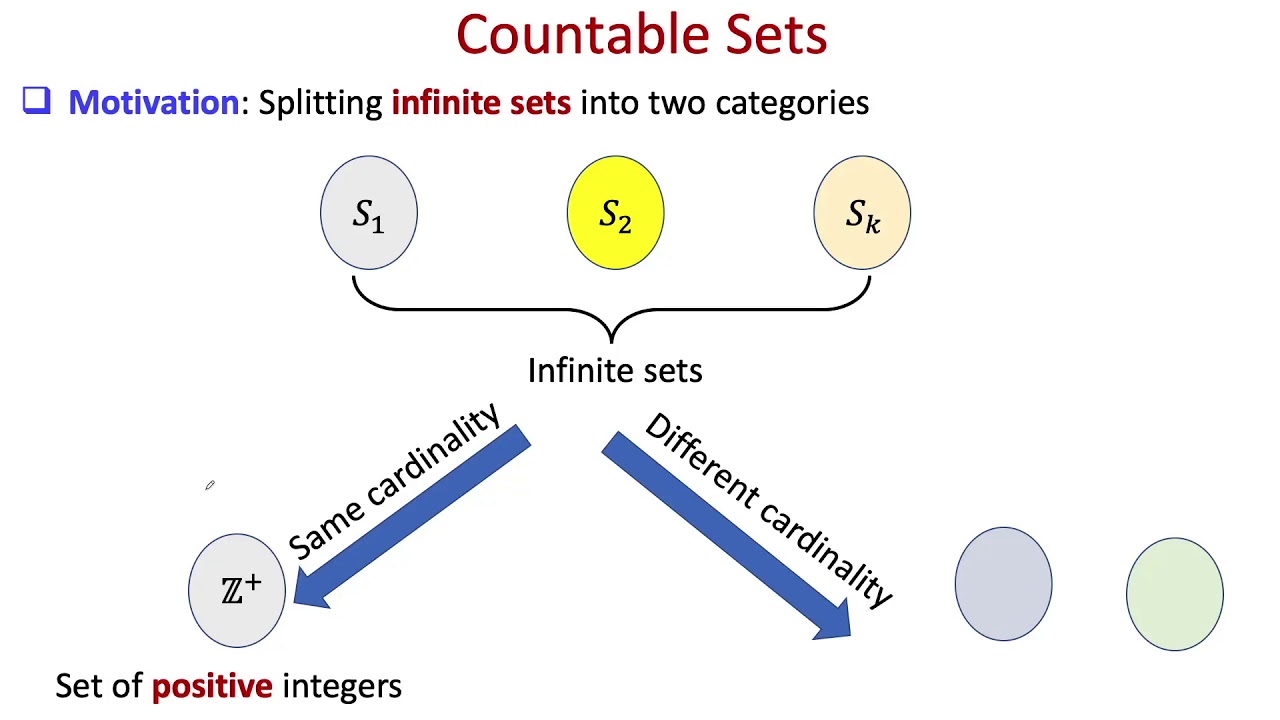
Is every finite set countable? Let’s explore this question by examining two scenarios.

First, consider a finite set A. In this case, the cardinality of any set B, denoted as |B|, is less than or equal to the cardinality of A, |A|. Since |A| is finite, |B| is also finite, and therefore, B is countable.

Now, let’s turn our attention to the case where A is countably infinite. This means that we can list all the elements in A. To determine whether B, a subset of A, is countable, we follow a simple process. We start with our list of elements in A, and by removing any elements that are not in B, we obtain a list specifically for B. Since the process of creating this list is systematic and preserves the order of elements, we can conclude that B is countable.