Can A Graph Have Exactly Five Vertices Of Degree 1? Exploring Graph Theorys Fascinating Puzzle
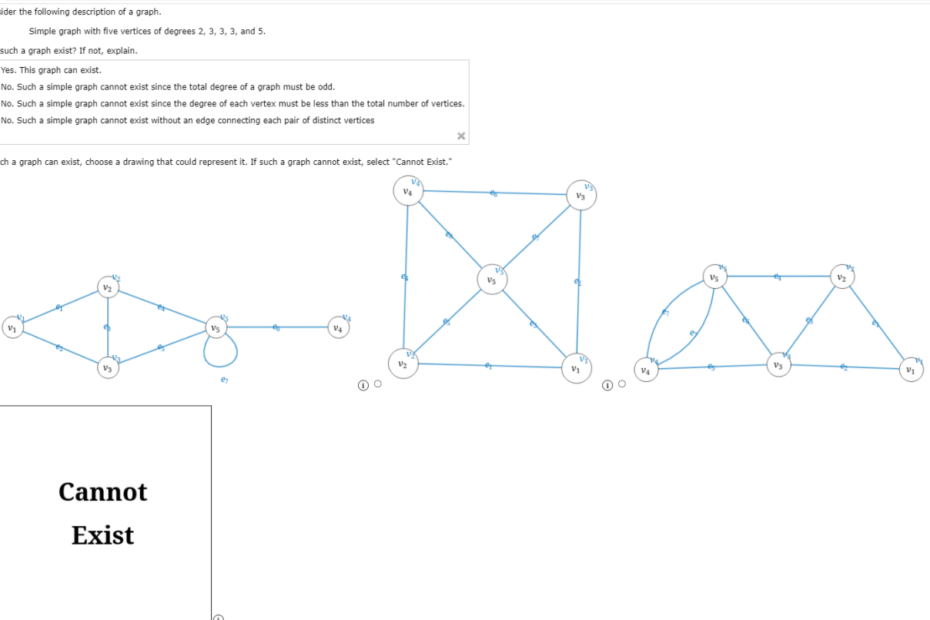
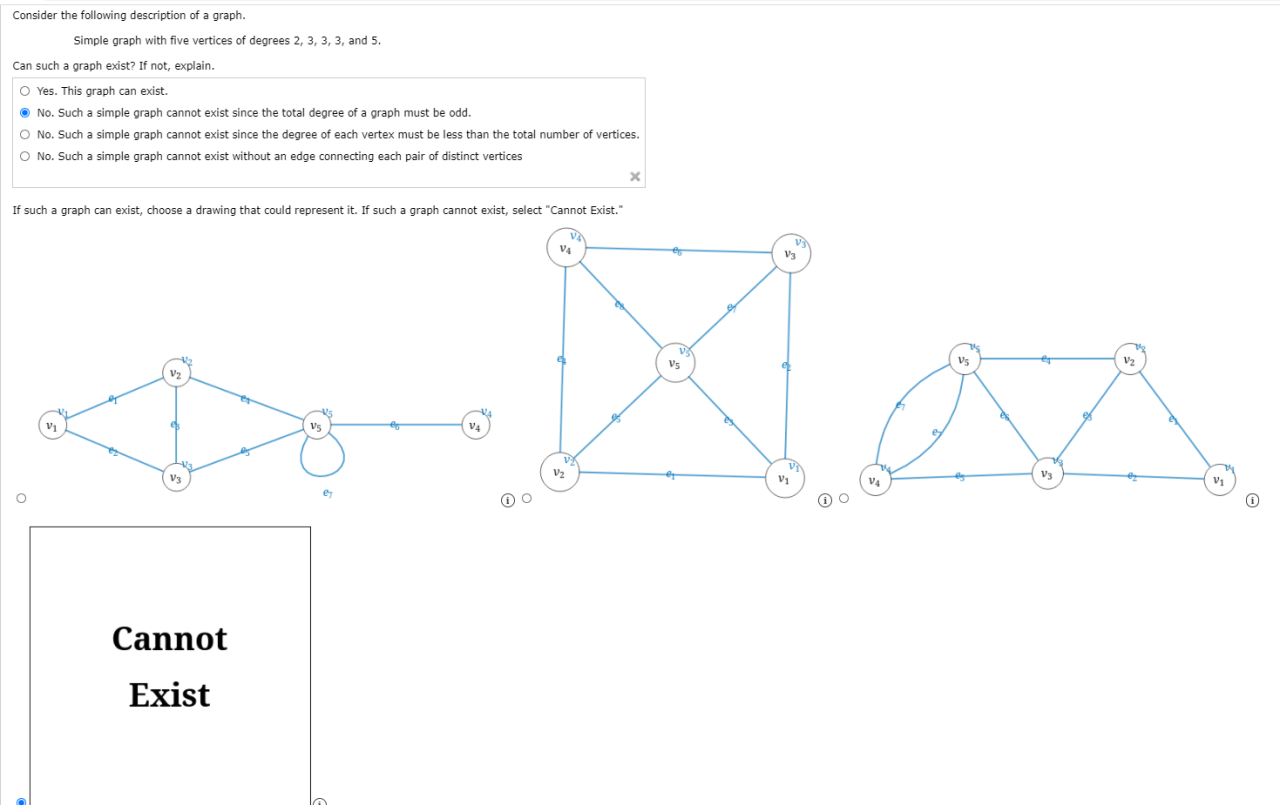
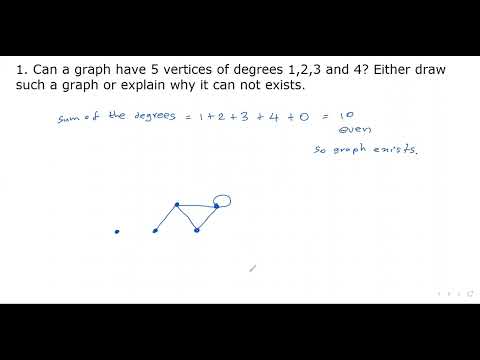
Can A Graph Have 5 Vertices Of Degrees 1, 2, 3, 4 And 5? Either Draw Such A Graph Or Explain Why It
Keywords searched by users: Can a graph have exactly five vertices of degree 1 Let G be a graph prove that there must be an even number of vertices of odd degree, simple graph with five vertices of degrees 1, 1, 1, 2, and 3., simple graph with six edges and all vertices of degree 3, find the degree of each vertex in the graph below, vertices and edges in graph, how to count edges in a graph, draw graph given vertices and edges, how to find degree of vertex
Can A Simple Graph Have 5 Vertices?
Is it possible for a simple graph to have 5 vertices? Yes, indeed! In fact, there are a total of 34 simple graphs that can be constructed using 5 vertices. Out of these 34 graphs, 21 of them are connected, meaning that every vertex in these graphs is reachable from every other vertex. If you’re interested in exploring these graphs in more detail, you can check out the provided link for visual representations and additional information. Additionally, among the 5-vertex connected graphs, there are specifically four of them in which every vertex has an even degree (meaning they are connected to an even number of other vertices). This information was last updated on January 6th, 2018.
Does There Exist A Simple Graph With 5 Vertices Of Given Degree I 1 2 3 4 4?
Is it possible to create a simple graph using five vertices with degrees 1, 2, 3, 4, and 4? Unfortunately, constructing such a graph is not feasible. A simple graph prohibits parallel edges (multiple connections between the same pair of vertices) and loops (connections from a vertex to itself). With only five vertices available, each vertex can connect to a maximum of four other vertices since there are no loops or parallel edges allowed. Consequently, it is impossible to have a vertex with a degree of 5 in this context.
Share 6 Can a graph have exactly five vertices of degree 1



Categories: Details 43 Can A Graph Have Exactly Five Vertices Of Degree 1
See more here: maucongbietthu.com
Learn more about the topic Can a graph have exactly five vertices of degree 1.