ระบบ สม การ ม 3
ระบบสมการ ม.3 หรือระบบสมการเชิงเส้นกับสถิติในระดับชั้นมัธยมศึกษาตอนปลาย เป็นสถาบันการเรียนการสอนที่รวบรวมรายวิชาคณิตศาสตร์และวิทยาศาสตร์ที่ใช้ในสายการเรียนวิทย์-คณิตศาสตร์ ซึ่งมีชื่อเต็มว่า “ภาควิชาคณิตศาสตร์และสถิติ” เป็นรายวิชาที่นักเรียนทุกคนต้องเรียน ซึ่งทำให้เป็นหนึ่งในรายวิชาที่มีการเรียนแค่ระดับชั้นไม่ต่ำกว่า Level 1 สูงสุดเพียงแต่มีการใส่แบบฝึกหัดในระดับชั้นมากที่สุด หรือจะอภิปราย สรุปก็คือในระดับชั้นมัธยมศึกษาตอนปลายระบบสมการคือระบบตัวเลขที่กำหนดโดยสมการเชิงเส้น ซึ่งมีรูปแบบคือ y=ax+b โดยที่ a และ b คือค่าคงที่ที่กำหนดหรือใส่ค่าการใช้งานก่อนแล้ว
ความสำคัญของสมการ ม.3
สมการ ม.3 มีความสำคัญอย่างมากในการเรียนรู้ทั้งในวิชาคณิตศาสตร์และวิชาสามัญอื่น ๆ เพราะช่วยให้เราสามารถแก้ปัญหาได้อย่างมีระเบียบ และให้เครื่องมือสำหรับการพิสูจน์ความเป็นจริงและการตรวจสอบทฤษฎีต่าง ๆ ด้วย
วิธีการแก้สมการ ม.3 ด้วยวิธีการต่าง ๆ
สมการ ม.3 สามารถแก้ได้โดยใช้วิธีการต่าง ๆ ซึ่งประกอบด้วยหลายวิธี อาทิเช่น วิธีของ Gauss, วิธีการปรับปรุงและวิธีการเวกเตอร์ เป็นต้น การแก้สมการต่าง ๆ นี้มีความสามารถที่แตกต่างกัน ยกตัวอย่างเช่น วิธีของ Gauss สามารถแก้ได้หลายเพราะสามารถตรวจสอบหากพบสมการที่ไม่ต้องการตอบหากแก้ได้
วิธีการใช้สมการ ม.3 เพื่อแก้ปัญหาในคณิตศาสตร์และวิชาสามัญอื่น ๆ
การใช้สมการ ม.3 ในคณิตศาสตร์และวิชาสามัญอื่น ๆ สามารถช่วยให้เราสามารถแก้ไขปัญหาที่สำคัญได้อย่างมีประสิทธิภาพ ยกตัวอย่างเช่น ในคณิตศาสตร์สมการ ม.3 สามารถใช้ในการหาคำตอบของปัญหาที่สมการจะต้องเป็นจริง ในวิชาสามัญอื่น ๆ สมการ ม.3 สามารถช่วยในการแก้ไขปัญหาที่เกี่ยวกับการวิเคราะห์วิทยาศาสตร์ เช่น ใช้ในการคำนวณทางสถิติ เป็นต้น
คุณสมบัติที่น่าสนใจของสมการ ม.3
สมการ ม.3 มีคุณสมบัติที่น่าสนใจอย่างมาก อันที่สำคัญต่อการใช้งานในชีวิตประจำวัน กล่าวคือสามารถแปลงสมการเชิงเส้นเป็นรูปของกราฟได้อย่างง่ายดาย หรือกล่าวอีกนัยหนึ่งก็คือสามารถใช้สมการ ม.3 ในการวิเคราะห์สมการเชิงเส้นและตรวจสอบว่าสมการถูกต้องหรือไม่ได้
การใช้สมการ ม.3 เพื่อแก้ปัญหาในด้านเศรษฐศาสตร์
ในด้านเศรษฐศาสตร์ สมการ ม.3 เป็นเครื่องมือที่สำคัญในการแก้ไขปัญหาตั้งแต่การวางแผนการเงิน การวิเคราะห์เศรษฐศาสตร์ การตัดสินใจทางเศรษฐกิจ การวิเคราะห์การเงินและการประเมินผล ฯลฯ ซึ่งการใช้สมการ ม.3 เพื่อแก้ไขปัญหาเศรษฐศาสตร์เป็นสิ่งที่รวมทั้งทางกลยุทธ์และวิธีการในอุตสาหกรรมที่เกี่ยวข้อง ในการใช้สมการ ม.3 เพื่อแก้ปัญหาเศรษฐศาสตร์จะสามารถทำได้โดยลดยอดวิเคราะห์ให้เป็นไปได้อย่างรวดเร็วและมีความแม่นยำที่สุด
การใช้สมการ ม.3 เพื่อแก้ปัญหาในด้านวิทยาศาสตร์
ในด้านวิทยาศาสตร์ สมการ ม.3 เป็นส่วนสำคัญในการแก้ไขปัญหาทางวิทยาศาสตร์ที่เกี่ยวข้องกับการการวิเคราะห์โครงสร้างของสายพันธุ์ การศึกษาการเคลื่อนที่ของวัตถุ การศึกษาที่เกี่ยวกับแรงดึงดูด การแก้ไขปัญหาที่มีอัตราการเปลี่ยนแปลง ฯลฯ การใช้สมการ ม.3 เพื่อแก้ปัญหาในด้านวิทยาศาสตร์สามารถใช้ในการวิเคราะห์การกระจายของกัมมันตภาพแสงของต่าง ๆ สามารถใช้สมการ ม.3 ในการวิเคราะห์ทฤษฎีของแรงไฟฟ้าและพลังงาน ฯลฯ
การใช้สมการ ม.3 เพื่อแก้ปัญหาในด้านบริหารธุรกิจ
ในด้านบริหารธุรกิจ สมการ ม.3 เป็นเครื่องมือที่จำเป็นในการแก้ไขปัญหาที่เกี่ยวข้องกับการวางแผนองค์กร การวิเคราะห์ความน่าเชื่อถือของข้อมูล การประเมินผลการดำเนินงานของบริษัท ฯลฯ การใช้สมการ ม.3 เพื่อแก้ไขปัญหาในด้านบริหารธุรกิจอาศัยหลักการได้เปรียบได้กับการใช้สมการ ม.3 เพื่อวิเคราะห์โครงสร้างความสัมพันธ์องค์กรภายใน สามารถนำไปใช้ในการทำนายผลกำไรของบริษัท การวิเคราะห์ข้อมูลเพื่อสร้างกลยุทธ์ทางการตลาด ฯลฯ
การใช้สมการ ม.3 เพื่อแก้ปัญหาในด้านวิศวกรรม
ในด้านวิศวกรรม สมการ ม.3 เป็นเครื่องมือที่จำเป็นในการแก้ไขปัญหาที่เกี่ยวข้องกับการออกแบบสิ่งประดิษฐ์ การวิเคราะห์ความสามารถในการดูแลบำรุงรักษา การออกแบบและการก่อสร้างโครงสร้างทางวิศวกรรม เช่น การออกแบบระบบไฟฟ้าในอา
ระบบสมการสองตัวแปร ม.3 | พี่วิว ติวเลข เรียนคณิต
คำสำคัญที่ผู้ใช้ค้นหา: ระบบ สม การ ม 3 ระบบสมการ ม.3 พร้อมเฉลย, ระบบสมการ ม.3 เพิ่มเติม, การแก้ระบบสมการเชิงเส้นสองตัวแปร ม.3 pdf, ข้อสอบ ระบบ สม การ ม.3 พร้อม เฉลย pdf, ระบบสมการเชิงเส้นสองตัวแปร ม.3 พร้อมเฉลย, การแก้ระบบสมการเชิงเส้นสองตัวแปร มีกี่วิธี, แบบฝึกหัดระบบสมการเชิงเส้นสองตัวแปร pdf, ระบบสมการเชิงเส้นสองตัวแปร ตัวอย่าง
รูปภาพที่เกี่ยวข้องกับหัวข้อ ระบบ สม การ ม 3

หมวดหมู่: Top 59 ระบบ สม การ ม 3
ดูเพิ่มเติมที่นี่: maucongbietthu.com
ระบบสมการ ม.3 พร้อมเฉลย
หัวข้อการเรียนรู้ในวิชาคณิตศาสตร์ระบบสมการสำหรับนักเรียนชั้นมัธยมศึกษาปีที่ 3 มีความสำคัญอย่างมาก เนื่องจากเป็นพื้นฐานที่จำเป็นในการเรียนรู้คณิตศาสตร์ในระดับสูงต่อไป นอกจากนี้ เรื่องระบบสมการยังเป็นเรื่องที่เกี่ยวข้องกับชีวิตประจำวันของเราอีกด้วย
ระบบสมการหมายถึงความสัมพันธ์ระหว่างสมาชิกของสมการ โดยทั่วไปแล้ว ระบบสมการจะประกอบไปด้วยสมการหลายสมการที่มีตัวแปรเดียวกันหรือตัวแปรหลายตัวสามารถแก้ไขหรือหาคำตอบที่เป็นไปได้ของระบบสมการเหล่านี้ได้
ในระดับชั้นมัธยมศึกษาปีที่ 3 ที่ถูกต้องนักเรียนจะได้เรียนรู้เกี่ยวกับระบบสมการที่มีตัวแปรเดียวกัน และมีการเรียนรู้เกี่ยวกับวิธีการแก้ไขระบบสมการด้วยวิธีต่างๆ เช่น วิธีประมาณ วิธีหาแบบตัวเลขแบบสมดุล วิธีตั้งปากกา วิธีคำนวณด้วยคอมพิวเตอร์ เป็นต้น
เพื่อให้นักเรียนเข้าใจและเรียนรู้ระบบสมการได้อย่างมีประสิทธิภาพ การเข้าใจตัวแปรเป็นสำคัญอย่างยิ่ง นักเรียนควรทราบถึงความหมายของตัวแปรในระบบสมการ ว่าแต่ละตัวแปรแทนอะไร และเหตุผลที่ต้องใช้ตัวแปรให้เขียนสมการเพิ่มขึ้น เช่น กำหนดให้ x แทนจำนวนนักเรียนชายในห้องเรียนและ y แทนจำนวนนักเรียนหญิงในห้องเรียน เมื่อมีสมการ x + y = 50
นอกจากนี้ การวางสมการเพื่อแก้ไขระบบสมการก็เป็นขั้นตอนที่สำคัญ นักเรียนควรเรียนรู้วิธีการตั้งสมการด้วยการใช้ประโยชน์จากปัญหาที่กำหนดให้ เช่น กรณีที่สมการต้องการคำตอบของจำนวนนักเรียนชายและนักเรียนหญิงในห้องเรียนสูงสุด หรือกรณีที่ต้องการหาอัตราส่วนระหว่างจำนวนนักเรียนชายและหญิงในห้องเรียน เป็นต้น
เมื่อความรู้เกี่ยวกับระบบสมการนี้เข้าใจแล้ว สามารถใช้เพื่อแก้ปัญหาในชีวิตประจำวันได้ ตัวอย่างเช่น การแก้ไขปัญหาทางคณิตศาสตร์ที่เกี่ยวข้องกับอัตราการผลิตพืชหรือสัตว์ กฎหมายที่เกี่ยวข้องกับการแจกแจงทรัพย์สิน การวางแผนการออมเงินและการลงทุน เป็นต้น
FAQs
1. ระบบสมการคืออะไร?
ระบบสมการหมายถึงความสัมพันธ์ระหว่างสมาชิกของสมการ โดยประกอบไปด้วยสมการหลายสมการที่มีตัวแปรเดียวกันหรือตัวแปรหลายตัว
2. ทำไมระบบสมการสำคัญต่อชีวิตประจำวัน?
ระบบสมการเป็นเรื่องที่เกี่ยวข้องกับการแก้ปัญหาในชีวิตประจำวัน เช่น การแจกแจงทรัพย์สิน การวางแผนการเงิน และการออมเงิน ซึ่งเป็นความรู้ที่สามารถนำไปใช้ในชีวิตจริง
3. วิธีการแก้ระบบสมการมีอะไรบ้าง?
มีหลายวิธีเช่น วิธีตั้งปากกา วิธีประมาณ วิธีหาแบบตัวเลขแบบสมดุล และวิธีคำนวณด้วยคอมพิวเตอร์ นักเรียนสามารถเลือกใช้วิธีที่เหมาะสมกับสถานการณ์และปัญหาที่กำหนดให้
4. ควรทราบอะไรเพิ่มเติมเกี่ยวกับระบบสมการ?
การเข้าใจและการใช้ตัวแปรให้ถูกต้องเป็นสิ่งสำคัญ นอกจากนี้ การวางสมการเพื่อแก้ไขระบบสมการก็เป็นขั้นตอนที่สำคัญในการแก้ปัญหา
5. สามารถใช้ระบบสมการแก้ไขปัญหาในชีวิตประจำวันได้อย่างไร?
ระบบสมการสามารถนำไปใช้ในการแก้ไขปัญหาทางคณิตศาสตร์ที่เกี่ยวข้องกับอัตราการผลิตพืชหรือสัตว์ การวางแผนการออมเงินและการลงทุน และข้อกำหนดทางกฎหมาย เป็นต้น
ระบบสมการ ม.3 เพิ่มเติม
บทนำ:
ระบบสมการ ม.3 เพิ่มเติมเป็นหนึ่งในเนื้อหาของวิชาคณิตศาสตร์ในระดับชั้นมัธยมศึกษาปีที่ 3 ในหลักสูตรและหนังสือเรียนของกระทรวงศึกษาธิการ หัวข้อหลักในระบบสมการเน้นไปที่การแก้สมการและอสมการ เพื่อให้นักเรียนมีความรู้ความเข้าใจพื้นฐานในเรื่องราวของเครื่องมือทางคณิตศาสตร์ที่ช่วยในการแก้ไขปัญหาหรือสถานการณ์ในชีวิตประจำวันโดยเฉพาะ
การเรียนรู้ระบบสมการม.3เพิ่มเติม:
ในหัวข้อระบบสมการส่วนเพิ่มเติม นักเรียนจะได้เรียนรู้วิธีการหาคำตอบของสมการสองประเภทคือ ระบบสมการเชิงเส้นและ ระบบสมการอนุพันธ์ โดยในการหาคำตอบของระบบสมการเชิงเส้นนักเรียนจะใช้เครื่องมือช่วยเพื่อแก้ปัญหาดังกล่าวได้อย่างสะดวกและรวดเร็ว
เครื่องมือทางคณิตศาสตร์:
1. กระดาษกริด: เครื่องมือแรกที่นักเรียนจะเรียนรู้ในการแก้ไขสมการเชิงเส้น ผ่านกระดาษกริดจะช่วยให้นักเรียนสามารถสังเกตและอธิบายความสัมพันธ์ระหว่างจำนวนที่เพิ่มขึ้นหรือลดลงในระบบสมการได้
2. การแก้สมการโดยใช้ตำแหน่งสังเกตปัญหา: เครื่องมือนี้ช่วยให้นักเรียนสามารถกำหนดตำแหน่งของจุดที่สอดคล้องกับสมการได้ ในกรณีที่เรามีสมการมากกว่าหนึ่งสมการที่เกี่ยวข้องกัน นักเรียนจะสามารถใช้เครื่องมือนี้ในการอธิบายตำแหน่งที่ทำให้สมการทั้งหมดสอดคล้องกันตามหลักของสมการการแก้การสอบในระบบสมการเชิงเส้นขั้นพื้นฐาน
3. การแก้สมการโดยใช้กราฟแสดงเป็นแนวด้าน: เครื่องมือนี้ช่วยให้นักเรียนสามารถแสดงสมการและเปรียบเทียบค่าราวกับสมการที่สอดคล้องหรือไม่สอดคล้องเชิงเส้น
4. การแก้สมการโดยใช้คำสั่งบอกค่าเชิงเส้น: เครื่องมือนี้ช่วยให้นักเรียนสามารถสังเกตและอาจารย์สามารถแสดงสมการเส้นตรงและค่าราวของสมการเชิงเส้นได้
คำถามที่พบบ่อย (FAQs):
1. ระบบสมการเฉพาะคืออะไร?
ระบบสมการเฉพาะคือระบบสมการที่มีความสัมพันธ์สมมติระหว่างสมการที่เขียนไว้ในรูปʃ ถ้ามีสมการมากกว่าหนึ่งสมการที่อธิบายความสัมพันธ์เชิงเส้นตรงกันก็เรียกว่าระบบสมการเฉพาะ
2. ระบบสมการอนุพันธ์คืออะไร?
ระบบสมการอนุพันธ์คือระบบสมการที่เขียนในรูปʃ เมื่อมีสมการมากกว่าหนึ่งอันที่ไม่เป็นสมการเชิงเส้นตรงที่สอดคล้องกับรูปที่กำหนดให้ ก็เรียกว่าระบบสมการอนุพันธ์
3. ตำแหน่งสังเกตปัญหาคืออะไร?
ตำแหน่งสังเกตปัญหาคือการกำหนดตำแหน่งของจุดที่สอดคล้องกับสมการ เป็นเครื่องมือที่ช่วยให้เราสามารถระบุตำแหน่งของสมการได้
4. การแก้สมการโดยใช้กราฟแสดงเป็นแนวทศนิยมที่ปรากฏในกราฟของทศนิยมคืออะไร?
การแก้สมการโดยการสมการโดยใช้กราฟแสดงเป็นแนวด้านยาวในกรณีที่ค่าของสมการมีค่าเท่ากับค่าทศนิยมที่ปรากฏในกราฟ
5. คำสั่งบอกค่าเชิงเส้นคืออะไร?
คำสั่งที่ช่วยสำหรับการแสดงสมการเส้นตรงและค่าทีทางกราฟแกนเส้นตรงสามารถลงชื่อความรู้และคำสั่งที่ใช้ในการแสดงค่าราวของสมการเชิงเส้น
สรุป:
ระบบสมการ ม.3 เพิ่มเติมเป็นหนึ่งในหัวข้อในวิชาคณิตศาสตร์ซึ่งเน้นไปที่การแก้ไขสมการและอสมการ นักเรียนสามารถใช้เครื่องมือทางคณิตศาสตร์ต่างๆ เพื่อเข้าใจและแก้ไขปัญหาต่างๆ ในระบบสมการ เช่น กระดาษกริด, การแก้สมการโดยใช้ตำแหน่งสังเกตปัญหา, การแก้สมการโดยใช้กราฟแสดงเป็นแนวด้าน, และการแก้สมการโดยใช้คำสั่งบอกค่าเชิงเส้น กรณีนี้นักเรียนจะสามารถนำมาใช้ในการแก้สมการเชิงเส้นและอนุพันธ์อย่างมีประสิทธิภาพในชีวิตประจำวันของนักเรียนและช่วยในการพัฒนาทักษะทางคณิตศาสตร์อย่างมีประสิทธิภาพในประสบการณ์ความรู้การเรียนรู้และการมีส่วนร่วมในการแก้ไขปัญหาในชีวิตประจำวัน
เนื้อหาในบทความนี้จะช่วยให้ผู้อ่านทำความเข้าใจและรู้จักใช้งานระบบสมการ ม.3 เพิ่มเติมได้อย่างถูกต้องและมีประสิทธิภาพ
มี 22 ภาพที่เกี่ยวข้องกับหัวข้อ ระบบ สม การ ม 3.




![ตัวอย่างระบบสมการเชิงเส้น 2 ตัวแปร [วีดีโอ 12:26 นาที] - เรียนออนไลน์ที่เว็บ DekTalent.com ตัวอย่างระบบสมการเชิงเส้น 2 ตัวแปร [วีดีโอ 12:26 นาที] - เรียนออนไลน์ที่เว็บ Dektalent.Com](https://dektalent.com/images/includes/video-ss/1308-linear-equation-system-examples.jpg)



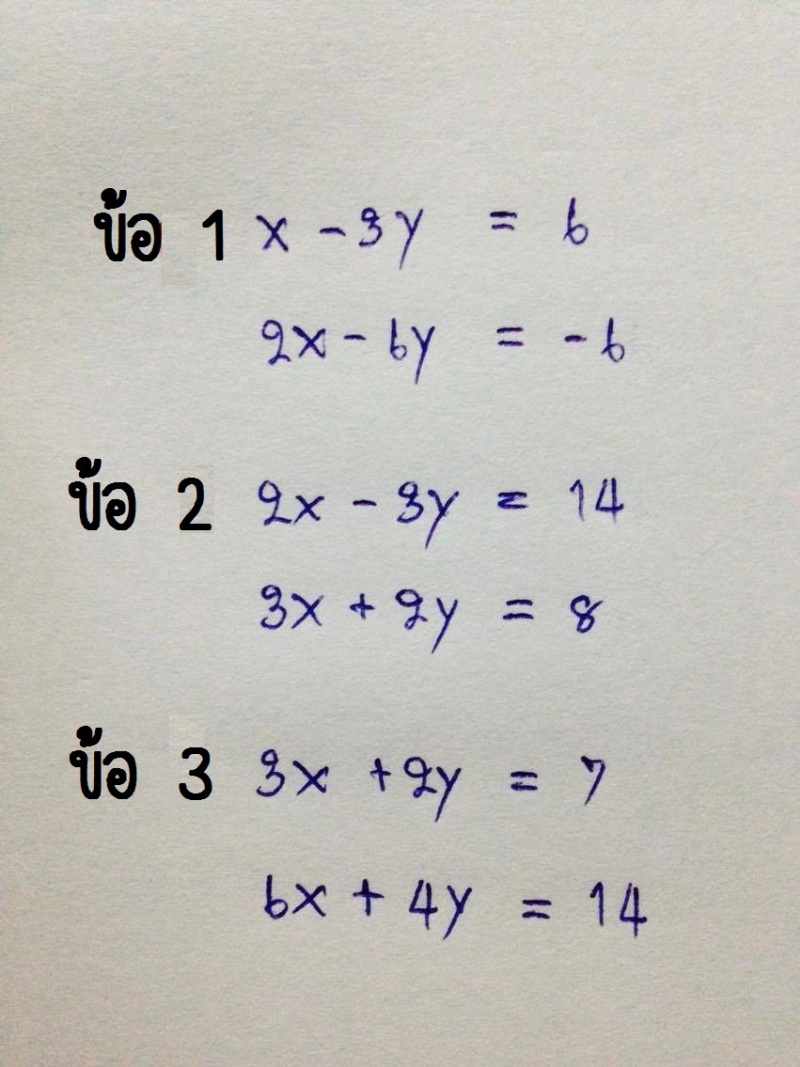



![ตัวอย่างที่ 3 - 4 การแก้ระบบสมการเชิงเส้นสองตัวแปร [วีดีโอ 10:14 นาที] - เรียนออนไลน์ที่เว็บ DekTalent.com ตัวอย่างที่ 3 - 4 การแก้ระบบสมการเชิงเส้นสองตัวแปร [วีดีโอ 10:14 นาที] - เรียนออนไลน์ที่เว็บ Dektalent.Com](https://dektalent.com/images/includes/video-ss/964-basic-equation-system.jpg)








![การแก้ระบบสมการกำลังสอง ข้อ 3-4 [วีดีโอ 9:26 นาที] - เรียนออนไลน์ที่เว็บ DekTalent.com การแก้ระบบสมการกำลังสอง ข้อ 3-4 [วีดีโอ 9:26 นาที] - เรียนออนไลน์ที่เว็บ Dektalent.Com](https://dektalent.com/images/includes/video-ss/1375-equation-system-solving.jpg)






















ลิงค์บทความ: ระบบ สม การ ม 3.
ดูข้อมูลเพิ่มเติมเกี่ยวกับโพสต์หัวข้อนี้ ระบบ สม การ ม 3.
- การแก้ระบบสมการเชิงเส้นสองตัวแปร – NockAcademy
- สรุป ระบบสมการเชิงเส้น ม.3… – คณิต by N-Knowledge | Facebook
- ระบบสมการเชิงเส้นสองตัวแปร
- คณิตศาสตร์ ม. ต้น ระบบสมการเชิงเส้นสองตัวแปร (ตะลุยโจทย์) โดยครู …
ดูเพิ่มเติม: https://maucongbietthu.com/category/after-hours